Recently I ran a math class for a few younger students, including my son. The objective of this class were to start making connections between how students visualize numbers and early arithmetic strategies.
Here are some of the various ways students visualized a group of dots to figure out how many total dots there were.

Here are some of the strategies students used when they doubled numbers in their pattern.
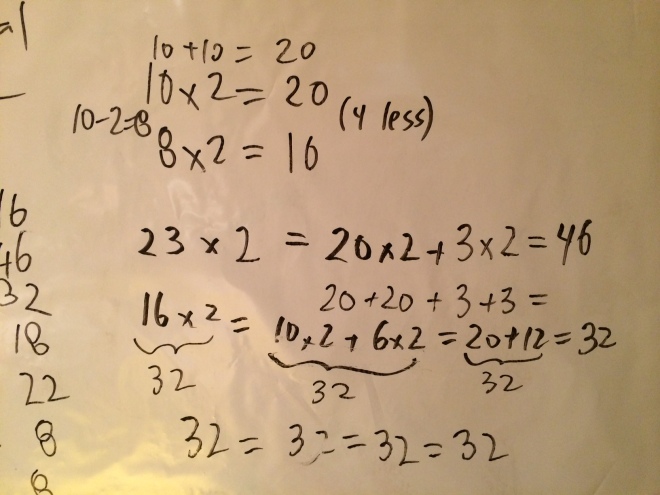
I asked students to look at the visualizations for the dot patterns and the arithmetic patterns and see if they noticed anything in common between the dot visualizations and the doubling strategies. They didn’t.
So I told them to find a partner, talk to their partner about the same questions, and then told them we would discuss it again. Two minutes later, I asked students to sit back down in the group after their discussions and re-asked the same question: “What is common to the strategies you (as a group) used for the dot visualizations and the doubling strategies? What is the same about what you did?”
One student said that in both cases, the students counted in order to find the answer, which was true. In both the dot visualizations and the doubling strategies, one strategy at least some students used was counting.
Another student said that in the dot pattern and the doubling strategies, we were trying to duplicate something. Not everyone knew what he meant by duplicating, so he explained it again, and I revoiced him and used the word doubling, which everyone understood.
Finally, another student had an epiphany. “When we did the dot pattern and when we did the doubling, something in common is that we figured out a big group and left some over to figure out at the end.”
Here are the actual two strategies he linked together with his observation:
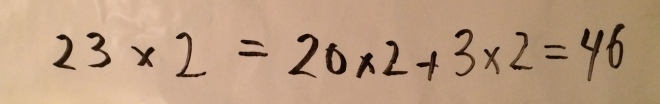
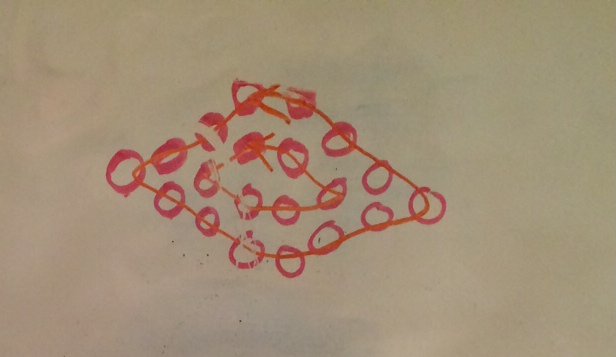
In the first one, in order to figure out 23 x 2, first we do 20 x 2 and we save the 3 to figure out later. In the second one, first we counted the perimeter and saved the inside shapes for later.
I’m excited by this observation as I had never thought of thinking of the distributive property as “saving part of the calculation” for later (although I have often seen other visualizations of the distributive properties).
